图灵完备部分游戏攻略
AI打牌
如果要机器人输,那也就是说,我得把它逼到它不得不取最后一张牌,最后一次行动,以及是,可以限制机器人跟我们之间的取牌,具体怎么限制呢?因为1到3张牌, 一回合我能做到固定一定能拿掉的牌数,是最大数加上最小数,也就是4张,比如说机器人拿1张,我就拿3张,刚好互补上,其他牌数量也一样,方针确定了,接下来就好办了, 1+4+4=9张,也就是说,我第一次就要取掉3张牌,再通过两次每回合
# take 3 poker
add_ii 0 3 7
# 4 poker per bout
add_i1 0 in reg0
sub_1i reg0 5 out
add_i1 0 in reg0
sub_1i reg0 1 out
我的汇编命名规则参照上一篇文章图灵完备游戏攻略4 不过,看了一下是真优雅,对比起随机存储器那关来说
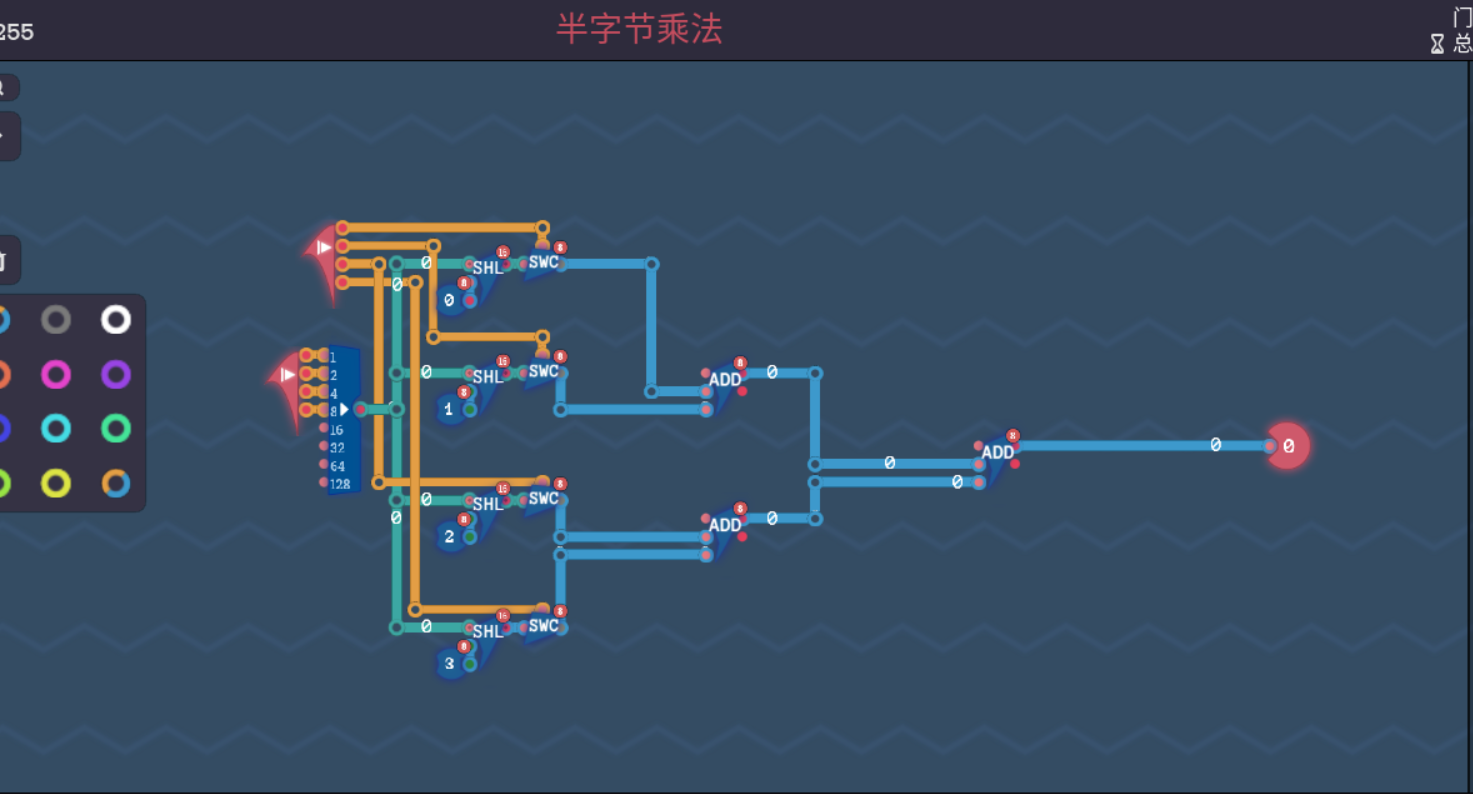
半字节乘法

解法其实挺简单的,因为已经被表示成二进制的数了,也就是说$a \cdot b$ 可以化成
a必定可以被表示成二进制,所以令$a = a_0 \cdot 2^0 + a_1 \cdot 2^1+a_2 \cdot 2^2+a_3 \cdot 2^3 , b = b_0 \cdot 2^0 + b_1 \cdot 2^1+b_2 \cdot 2^2+b_3 \cdot 2^3$
则 $ a \cdot b = (a_0 \cdot 2^0 + a_1 \cdot 2^1+a_2 \cdot 2^2+a_3 \cdot 2^3) \cdot (b_0 \cdot 2^0 + b_1 \cdot 2^1+b_2 \cdot 2^2+b_3 \cdot 2^3)$
其中的展开项,其中又有乘2以及2的倍数实际上就等于数字左移,也就是说,可以按一边当作操作数那样然后后面挨个加起来,再有
$(2^0+2^1+2^2+…+2^n) \cdot (2^0+2^1+2^2+…+2^m) = (2^n-1)(2^m-1) < 2^{n+m}$
所以两个4位二进制数一定不会在八位上溢出,add上的进位也不需要了,只需要直接加起来就行了
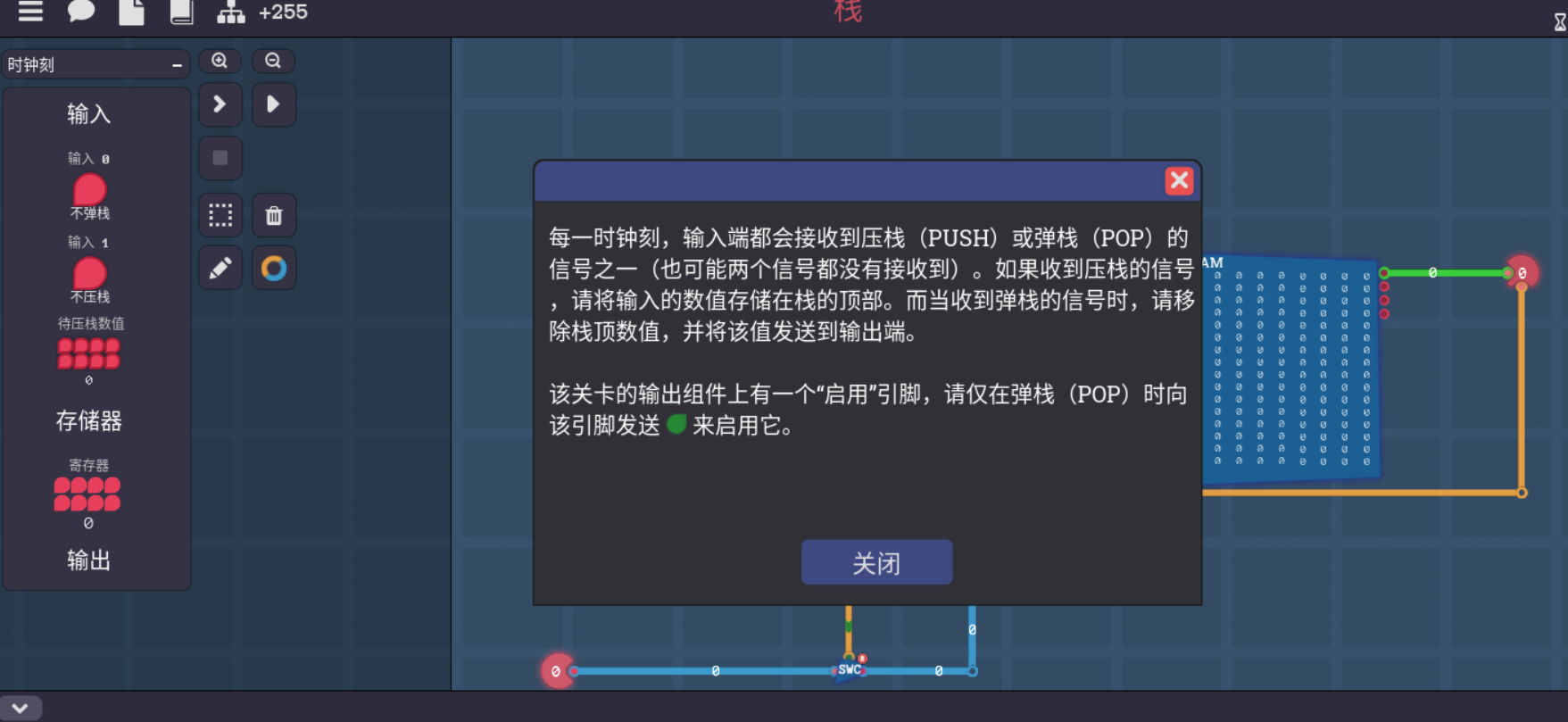
栈
写到这里,我其实还是挺希望我可以把我所有的思考步骤完整写下来的,但考虑到一方面比较花精力,另一方面感觉这也不是适合放在博客里的东西,有时候会太长了, 如果只是给我自己看我写这一些就已经够了,我也不知道看我博客的其他人是否多,但我感觉基本是我自己而已,有需要的话在我的B站私信或者评论区留言再考虑是否拿出来吧。
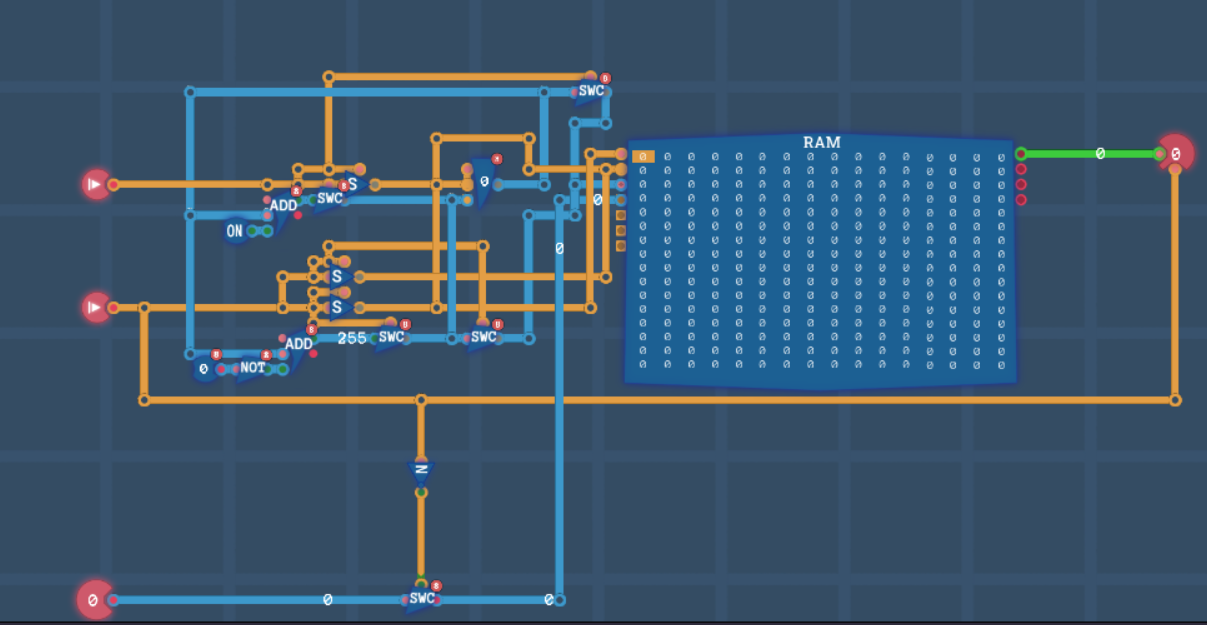
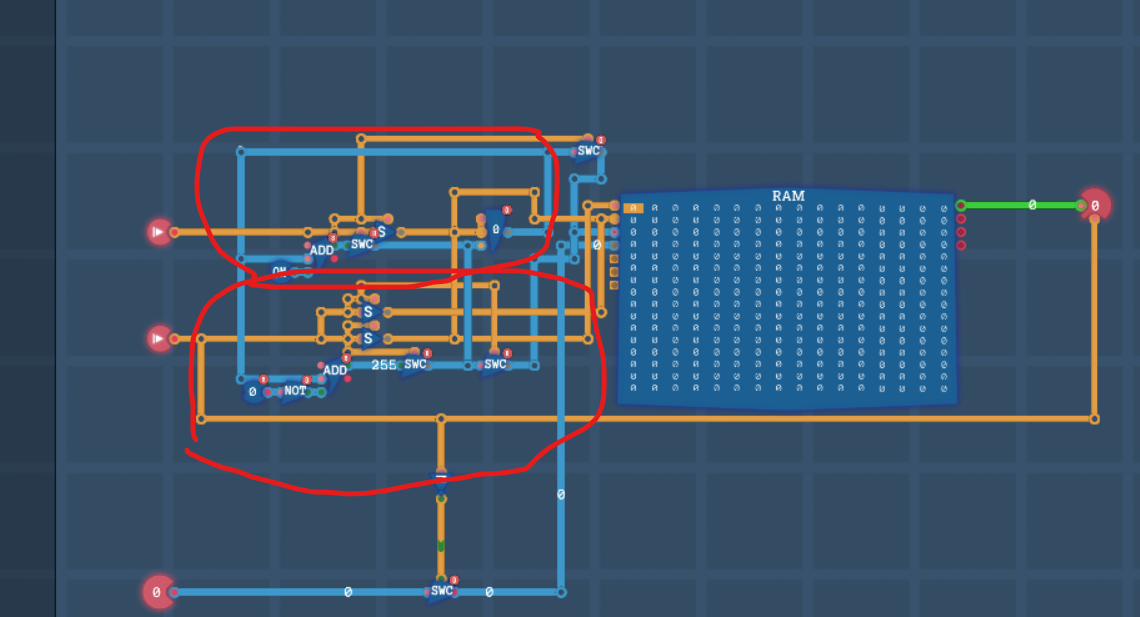
压栈
首先,先清楚两个操作要干什么,压栈和弹栈,分别是push和pop操作,push,也就是写入一个列表里面,想到栈我第一想到的是要用不小的存储空间,也就是先想到了内存, 毕竟寄存器也是只是临时存一下数据,空间毕竟还是太小了,但,根据前面写内存的经验来看,一般需要一个寄存器读取地址位,毕竟可以栈这个玩意,可以理解为指针放在某个位置然后在那附近进行读写或者擦除操作, 需要一个临时的存储工具,也就是寄存器,虽然整个任务比较复杂,但是这些东西构建的时候也不必慌张。
从简单的入手开始即可,比如我先从压栈操作开始实现,一旦压栈的信号电平变为高电平, 也就是开始执行压栈压入输入的数值,因为考虑到后面弹栈操作也会需要使用这个寄存器,然后再想到这个信号本身是个1bit的信号,如果不想影响其他信号可以通过这个信号到目标处添加一个开关, 然后通过这个信号来控制这个开关,那么一旦这路信号不通的时候,其他路信号控制寄存器的时候就可以被开关隔断,不过,一开始我是寄存器出来的数值直接读入内存寻址位的, 但是这部分在前面的关卡内存读写那边没写好是真的,因为内存初始值指针就是0,然后考虑到还需要累加,那么我在后面直接加入一个add 1就可以了,但是如果压栈操作信号处于低电平了, 我要求add不工作或者工作了输出,所以就有了那个add出门之后的开关,以及是,压栈开启时得开启内存的写入开关,把写入开关连上信号+开关后的输出即可,以及是需要输入端接上一个开关连到内存的输入部分即可
弹栈
弹栈的操作,第一是先输出完一次运算值,然后对这个值覆写0的操作,也就是其中要同时激活读和写的开关,读先是读出这个位置的数据,输出开关跟弹栈开关相连,压栈操作并不会控制它毕竟, 可以直接连,以及是对寄存器的操作,要求每次写入减1,先实现减1的操作,也就是寄存器输出的值回路连上减法器,减法器,add前面加not并不能直接实现,毕竟直接对1取反是254, 加2才会等于0,也就是说直接就是0位的取反,255,+1就等于0了,实际上是256-1,也就是说加号那边写255或者是0的取反,以及开关操作同上,
但有一点得注意的是,寄存器输出会有延迟,因为压栈的时候默认的值就是0所以才忽略不计了,然后默认每次+1,每次都可以按时写入,但读取并不是,比如说进行一次压栈操作,寄存器原来是0,输出也是0, 然后配合数值写入0位,寄存器写入1,但是此刻输出还是0,得等下一刻才会变成1,然后下一刻输出1的值,写入没关系,因为原本就放在那个位置,可以是先进行写入再移动指针等待下一刻的写入或者输出, 但弹栈不行,比如说我写入一次之后立刻进行弹栈,此时寄存器的输出是1,也就是原本的值,减法器输出0了,我们知道现在寄存器1的位置因为没有经过读写,是没有东西, 就是默认数值0的,但是我要读写1的位置怎么办呢?直接读写减号后面的输出,那已经经过运算变成0了,以及是输入处被我们禁用输入变成0了,此时可以直接同时接通读和写的开关, 先让输出要输出的值,然后写入0完成覆写,到这基本已经完成了,但是依旧有个小细节,就是,你的弹栈输出部分读和写并不能相连,一旦连上会导致压栈的时候,你一激活写的开关会把读的开关也一并激活了, (当时我输出的开关也连上了后面的线,导致输出也被激活了,实际不应该激活的,如果是直接输出没激活输出了其实也没事)所以我选择用另一个信号+开关的方式来分别激活读和写的信号位。 到此,两个功能就实现结束了
压栈和弹栈
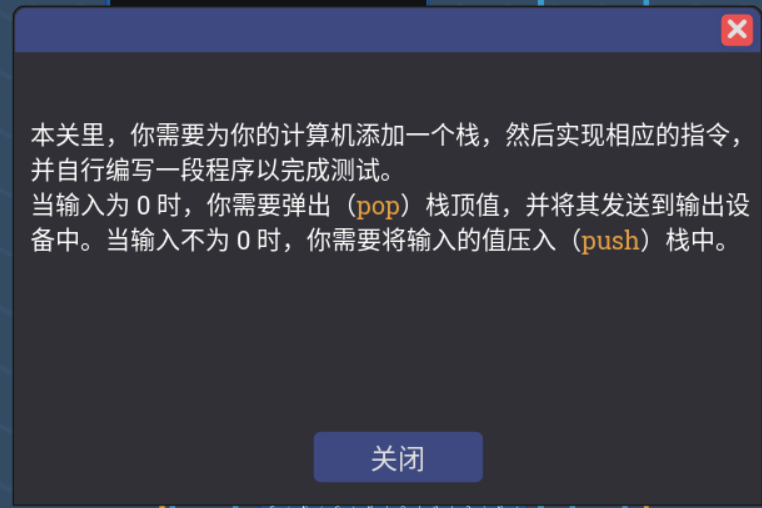
既然要集成到LEG体系内,就基本必须得给分配一位信号位了,我分配了一个16bit的信号位给压栈和弹栈,然后直接输入输出交互,但是为了以后的可操作性,我把第二位分配成了输入地址位, 然后第四位分配成了输出地址位,第三位置空,其中有个注意事项就是,一旦这一位栈位亮起,意味着前面的运算位的输出得受到抑制,以及是,输出接到第四位没过解码器之前, 然后通过最后一位进入输出位即可,其中下图上方部分得稍加判断输入信号的值
除法
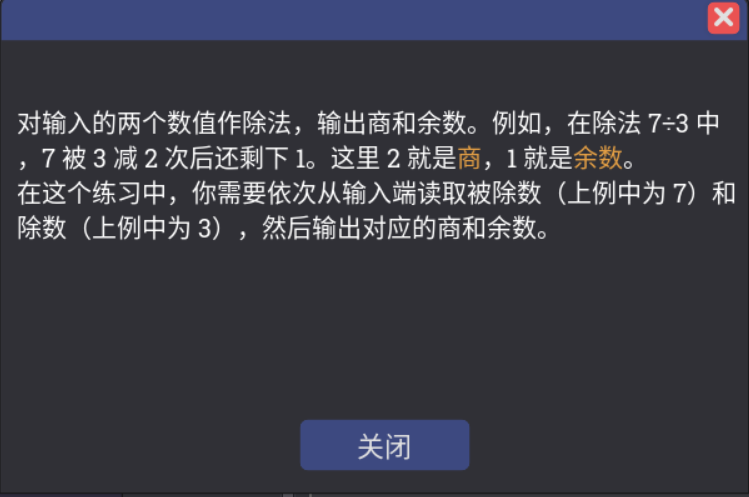
$29 \div 18= 1$ ,余数是11
思路方向:
$a = a_0 \cdot 2^0 + a_1 \cdot 2^1+a_2 \cdot 2^2+a_3 \cdot 2^3$
$b = b_0 \cdot 2^0 + b_1 \cdot 2^1+b_2 \cdot 2^2+b_3 \cdot 2^3$
令$a$为被除数吧,$b$为除数,现在的思路如下,先找结果最高位,其中在十进制中,小学的时候学过,除法是先对齐最高位,然后判断最高位处的大小 比如$732 \div 25$
$$ \begin{array}{r|r} & \text{29} \\ \hline \text{25}& \text{732} \\ & \text{-500} \\ \hline & \text{232} \\ & \text{-225} \\ \hline & \text{7} \end{array} $$类似于图中这样的计算过程,二进制也是一样的,十进制乘10就移动一位,二进制乘2就移动移位,计算规则其实一样, 不过最高位得看是否能除的下来,然后一位一位递减判断,能除下来就写1不能除就写0,但这有个例外就是0是被除数得输出错误
曾经我本来的想法是,第一个不可行了怎么样换第二个条件,实际就有点时间换空间的刻板印象了,实际则是条件$A$满足时运行,也就是$ABC…$ 然后如果$A$不成立,则补充$\overline{A}BC…$,其中$BC…$为其他条件,也就是意为A不成立时其他条件加入的情况来表示当前状态就可以了,带入到下面的状态就是, 左移被除数到对齐时最高位跟原数进行比较这个事件为$A$事件,然后$BC…$其余则是比它低的位的情况
$$ \frac{a}{b} = \frac {1 \cdot 2^m+a_{m-1} \cdot 2^{m-1}+...+a_0 \cdot 2^0} {1 \cdot 2^n+b_{n-1} \cdot 2^{n-1}+...+b_0 \cdot 2^0} $$(其中$m$和$n$分别为$a$和$b$的最高位,以及,设定$m>n$), 则
$$ \frac{a}{2^\frac{m} {n} \cdot b}= \frac {1 \cdot 2^m+a_{m-1} \cdot 2^{m-1}+...+a_0 \cdot 2^0}{1 \cdot 2^m+b_{n-1} \cdot 2^{m-1}+...+b_0 \cdot 2^{m-n}} $$此时如果$a>2^{\frac {m}{n}}\cdot b$则$2^{\frac {m}{n}}$此位大于$0$,输出的两数比较也就是用比较器比一下$a$和$2^{\frac{m}{n}} \cdot b$的大小即可, 如果大于则把该位标记1后减去$2^{\frac{m}{n}}\cdot b$然后进入低一位进行判断即可
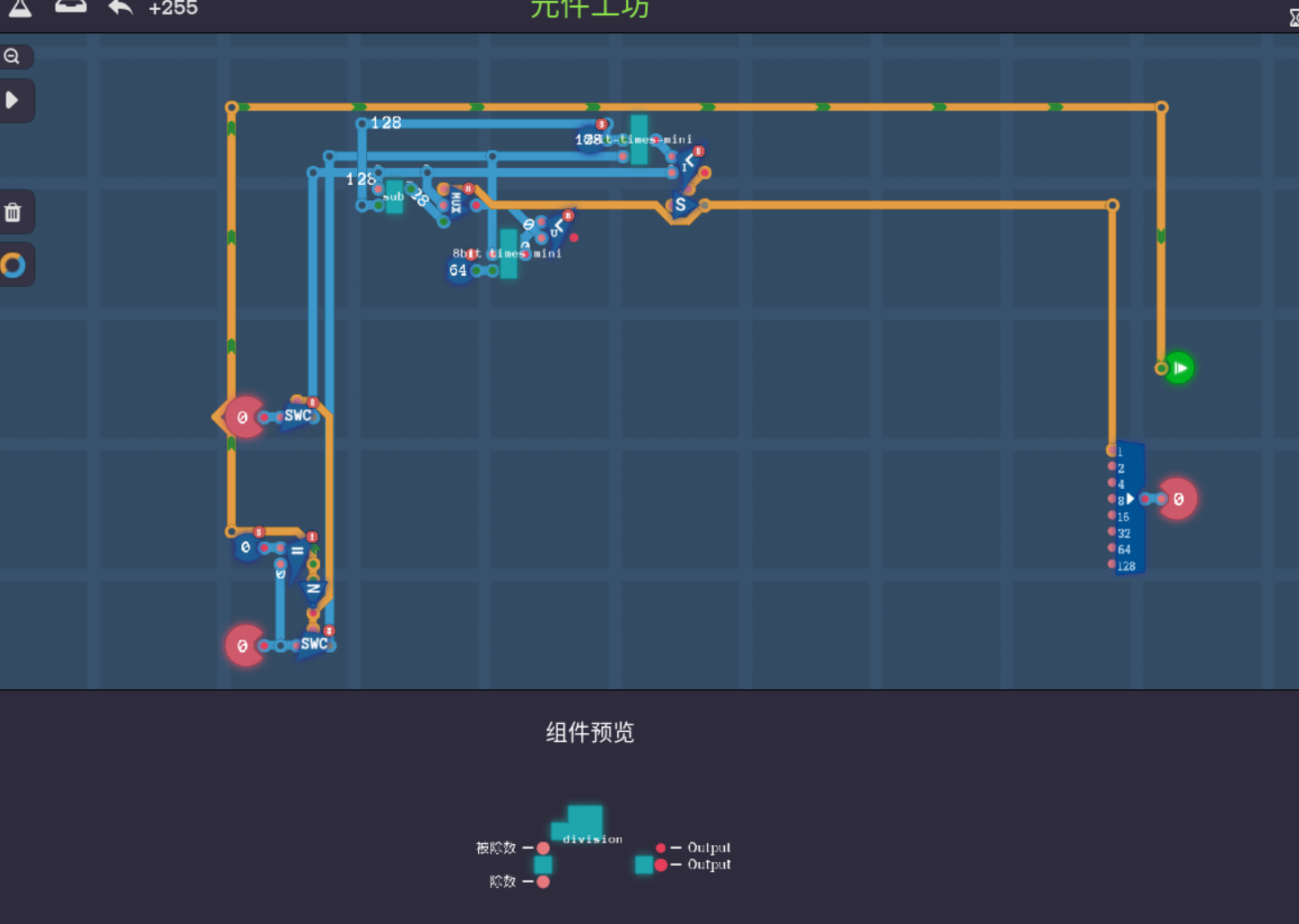
实际动手了之后发现可以有复用的地方,如果不复用一部分最后产生的除法运算器实在是太大了,而且线全部要自己拉,所以我选择复用一部分
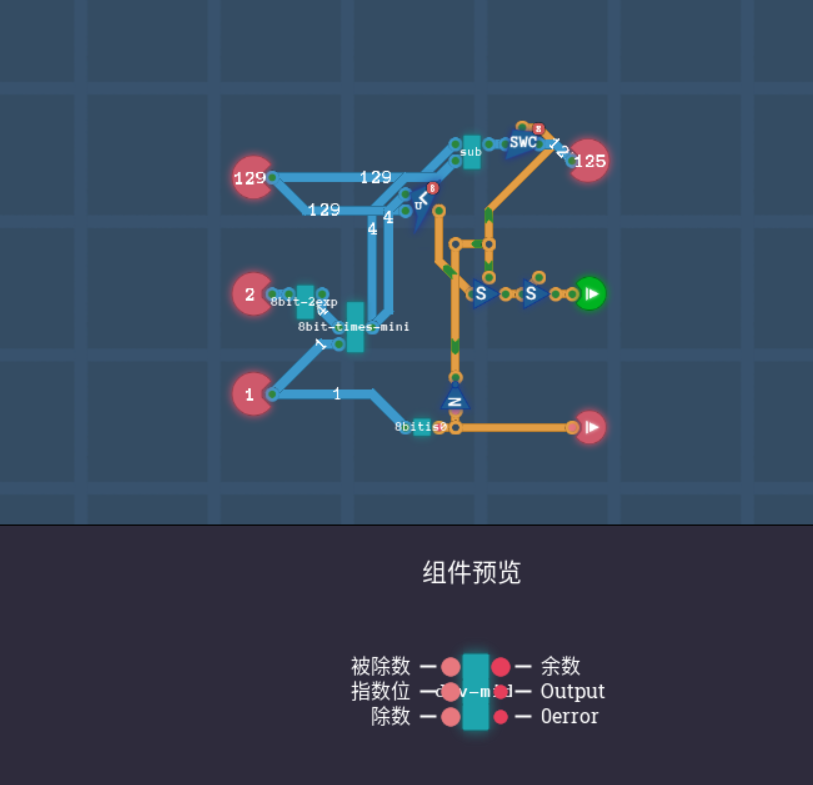
但我很快发现了问题,一旦除数和要取的位超过8bit,那么溢出之后将得不出结果了,于是我直接想着,既然已经有16位了,我干脆直接把我的乘法运算器也升级到16位算了, 于是,去调了一下乘法运算器,也就是把原本的16位合并进输出就可以了,如下
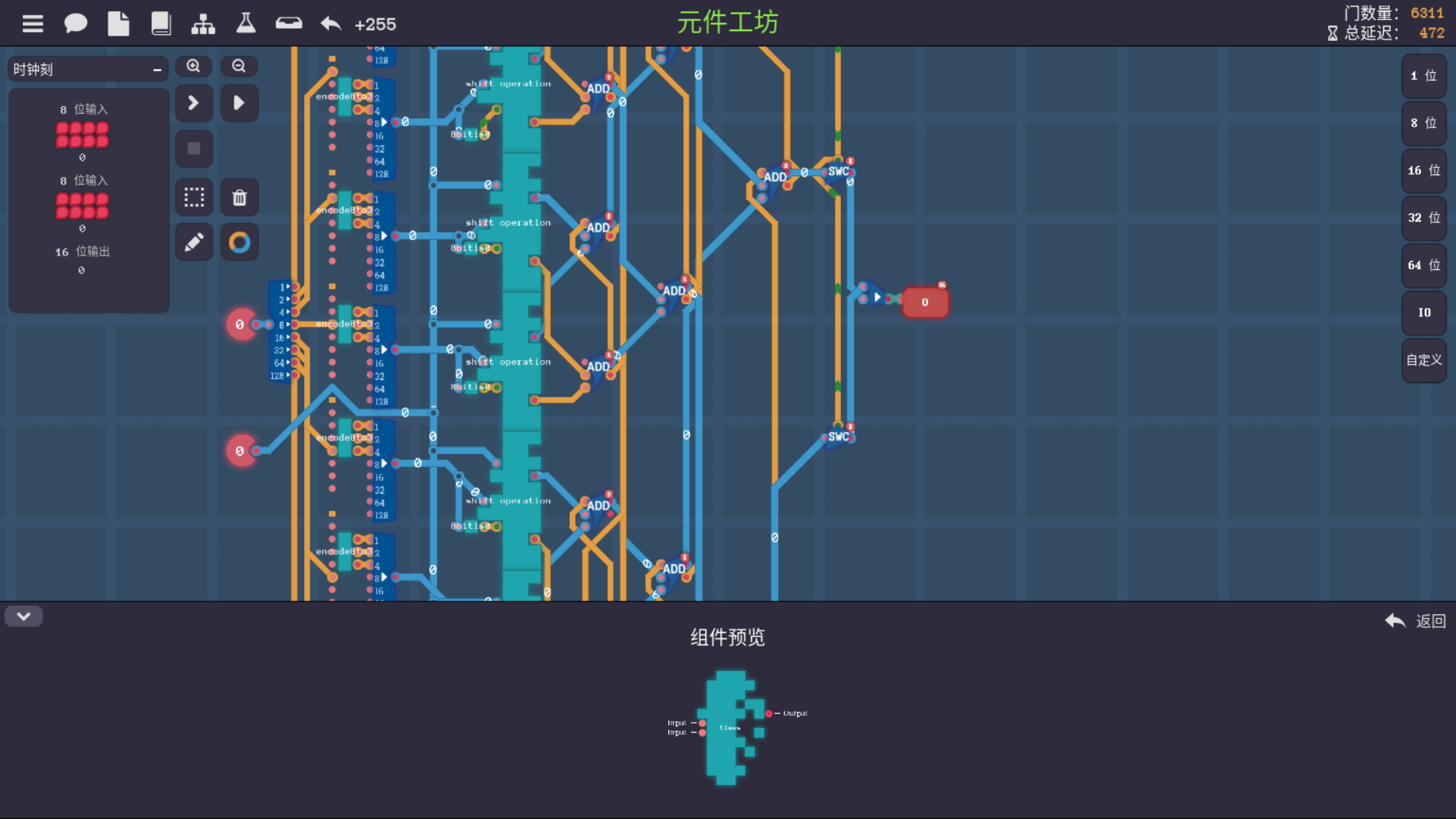
改动完之后发现,比较器如果不升级成16位的也没办法了,于是把比较器也换成了16位的,如果过于溢出就不必输出8位的了,因为被减数都是8bit的,输出也只要指定8bit就可以了, 以及其他的
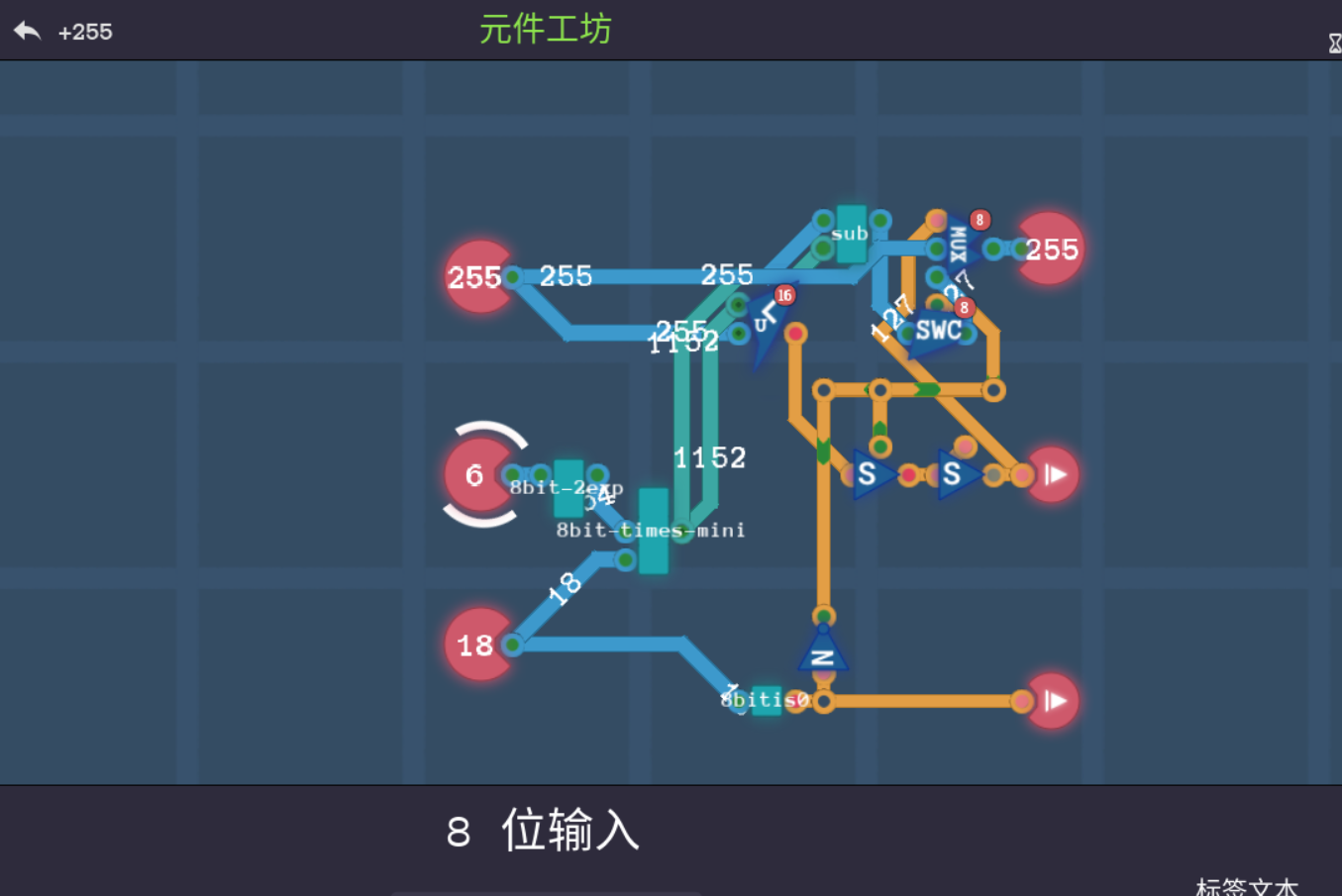
其中,如果一旦被除数是0,那么直接ban了其他两位的输出,所以需要开关,另外,排除掉除数是0的状态后,讨论一下输出位是0或者1的情况
- 如果是0,也就是说最高位移动后大于被除数,也就是类似$245 \div 50$这样,最高位处已经输出得是0了,那么余数就原样输出就可以,然后进行到下一轮的循环,也就是取下一位
- 如果是1,也就是说最高位移动后小于被除数,类似的对比则是$245 \div 22$,最高位输出是1,余数得输出两数相减,即$a-2^{\frac {m}{n}} \cdot b$
所以余数位得规划两路输出,一路是原数输出,另一路是两数相减的输出,启用一个二选一选择器即可
搞定完这些之后,除法处输出就轻松了,不用摆那么多东西了
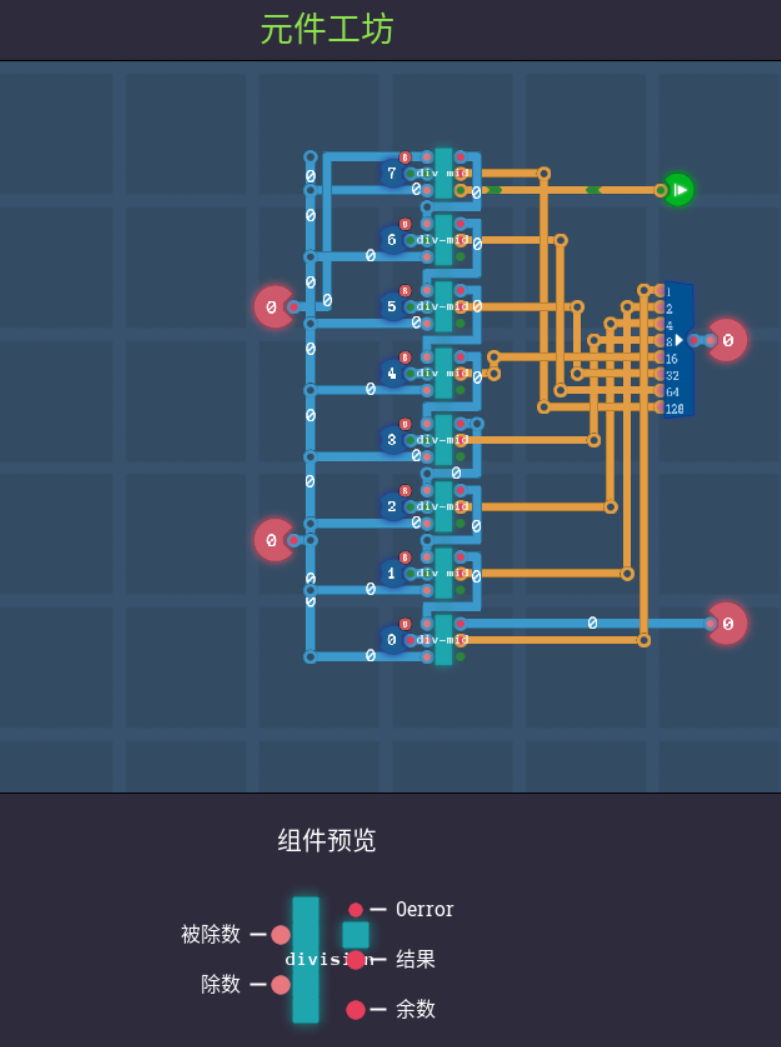
然后在LEG-ALU模块中加入除法运算器
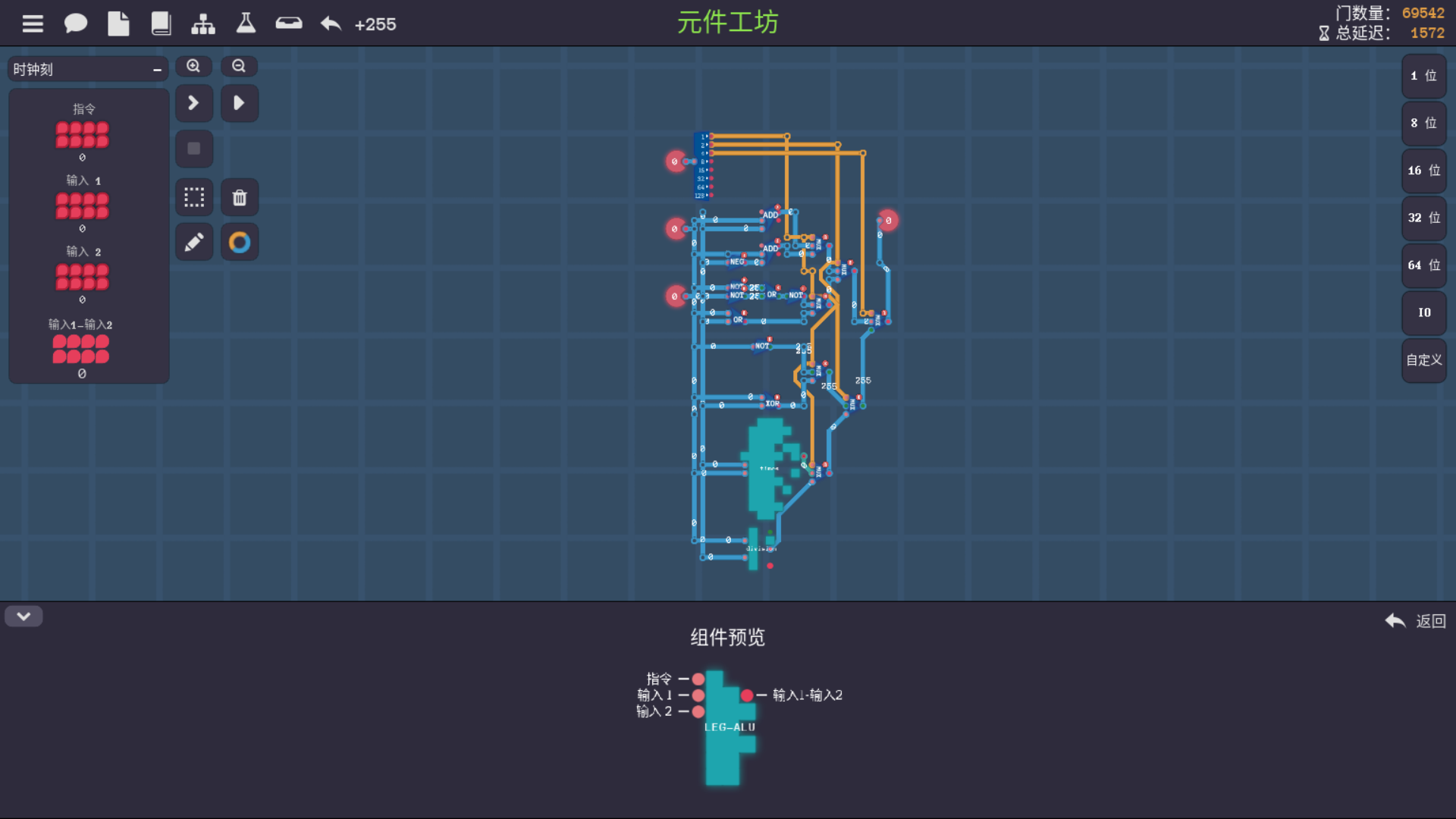
到最终这边测试的时候又发现一个问题,我真TM恨啊,你游戏开发者最后平衡也没顾好了,讲真,LEG-ALU里一堆用不上的玩意,塞里面,然后把我可能要用的运算吧, 塞的没法动了,搞的我原本搭好的逻辑框架不想再去动一下
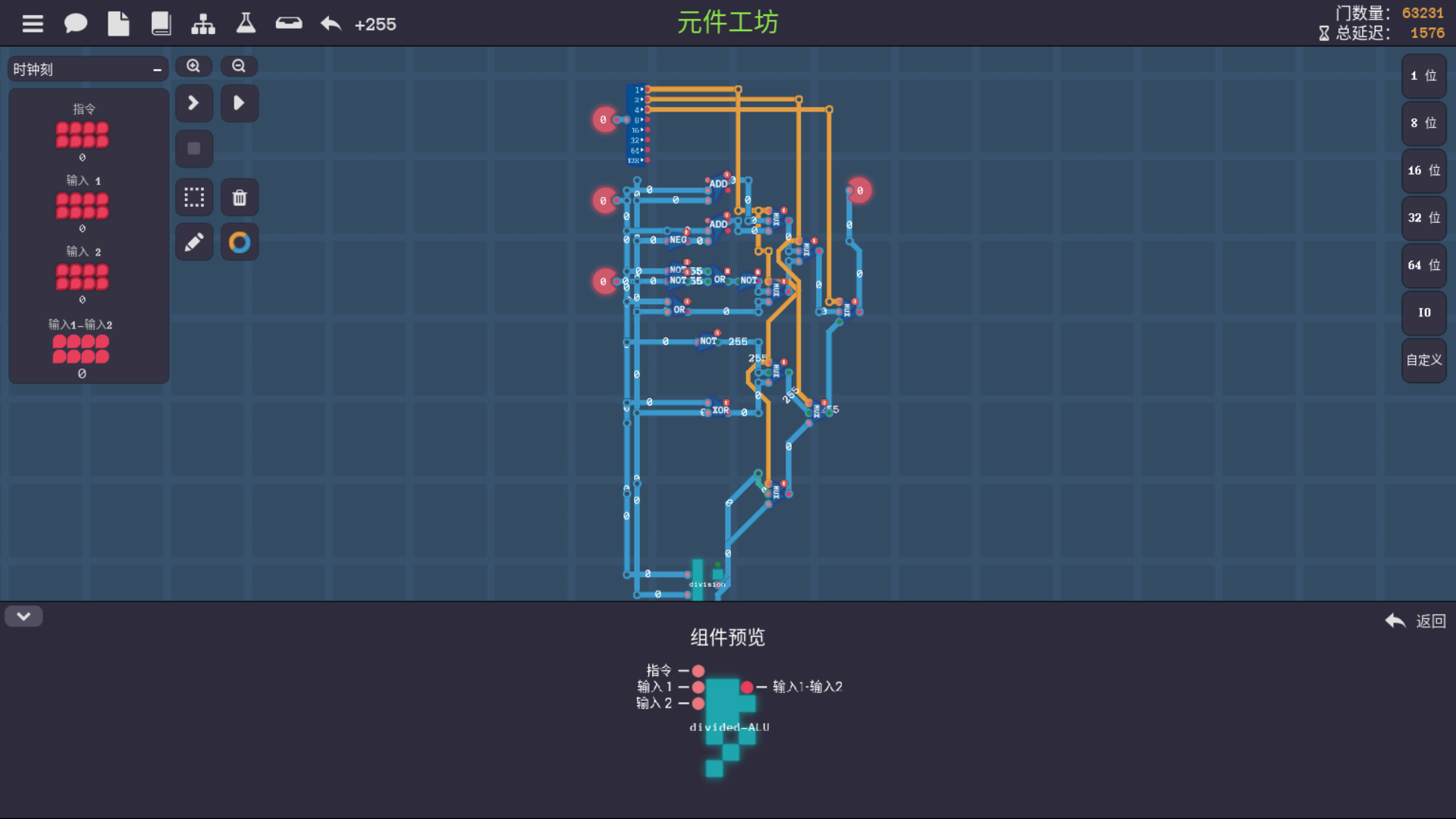
现在反正有存不同版本的LEG框架,干脆直接就是魔改一个divide版本的ALU出来算了,然后把原本的线路复制出来复制到一个单独的divide线,然后把改完的ALU替换掉原来的ALU,唯一麻烦的地方在于需要重新搞一下指令集
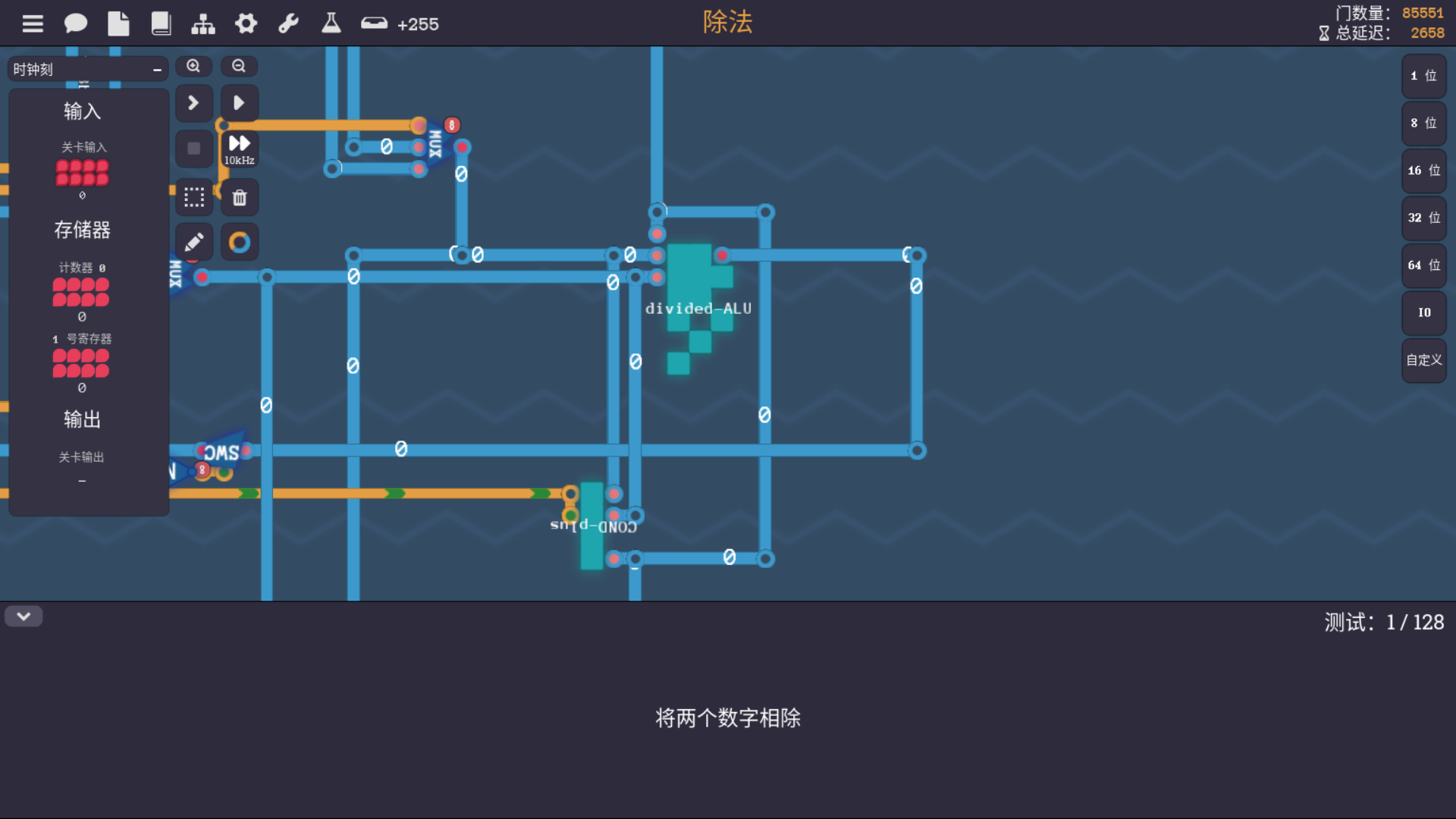
输入代码后发现依旧有错误,结果是发现div-mid的错误,才发现只有小于号,加了一个or算了,有时候不如自己写一个
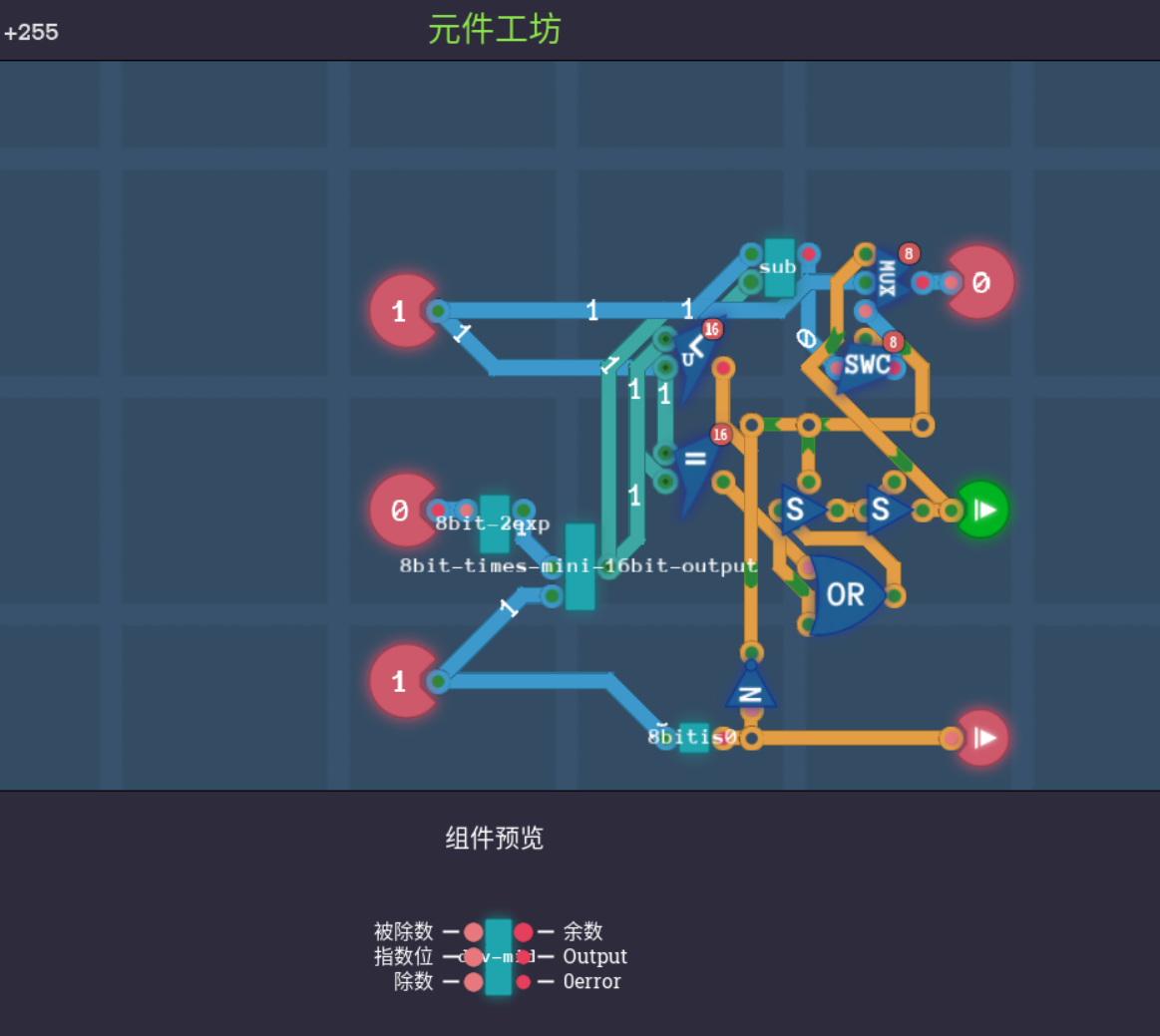
这样这一关就过了,拖了不少时间
